Ученый РУДН сравнил алгоритмы решения задачи оптимального управления
В системах, где есть несколько объектов, которым нужно задавать последовательность действий, возникает так называемая задача оптимального управления. Например, в задаче управления космическим кораблем или налоговой системой страны. Математически это означает, что нужно минимизировать или максимизировать какой-либо параметр системы (например, минимизировать время или максимизировать занятость населения). Общепринятого универсального способа численно анализировать такие системы не существует, однако есть множество подходов и алгоритмов. Исследователи РУДН и ФИЦ «Информатика и управление» РАН предложили два подхода на основе нескольких современных компьютерных алгоритмов для решения задачи оптимального управления группой роботов.
«Группа роботов должна перемещаться из заданных начальных состояний в конечные, избегая препятствий, за минимальное время. Задача относится к классу бесконечномерной оптимизации. Существует два класса методов ее численного решения. Прямые методы основаны на сведении к задаче конечномерной оптимизации. Непрямые методы основаны на применении принципа максимума Понтрягина для перехода к краевой задаче и её последующего численного решения», — Сергей Константинов, старший преподаватель департамента механики и процессов управления РУДН.
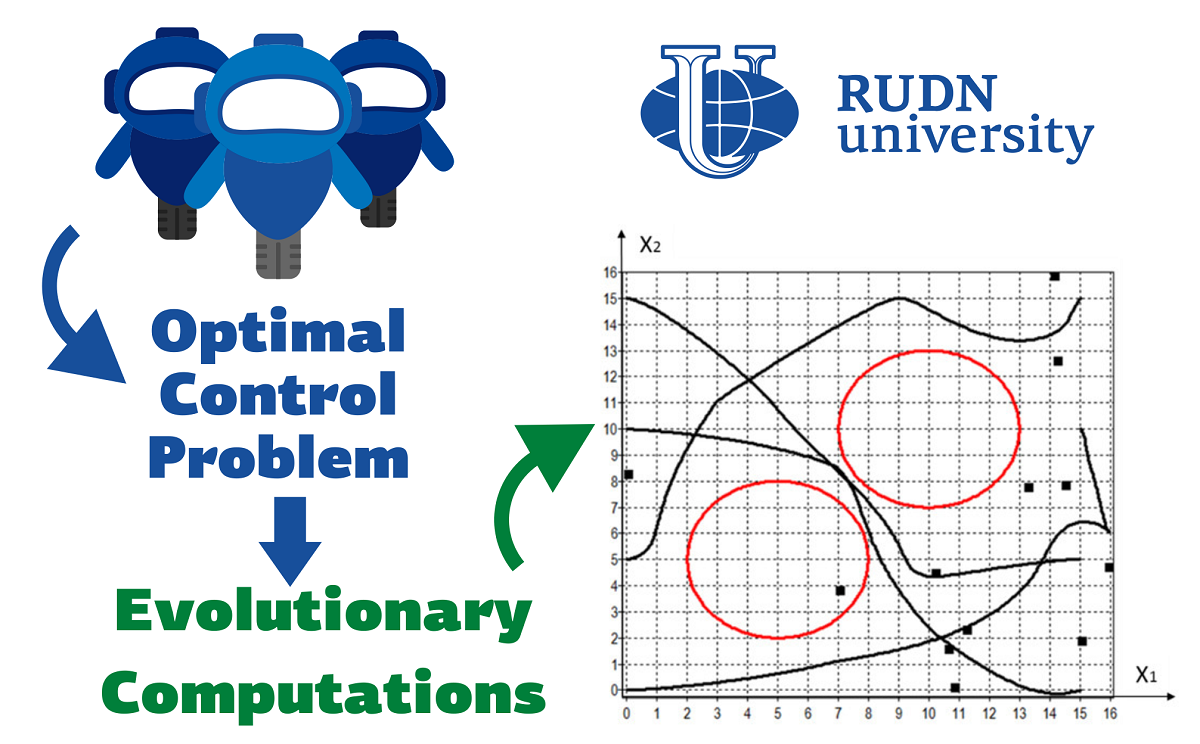
Ученые предложили два подхода к решению задачи оптимального управления на основе прямых методов. В тестовой задаче роботы должны переместиться из начальной точки в конечную и не столкнуться с препятствиями и другими роботами. В первом подходе группа роботов рассматривалась как один объект. Задача оптимального управления в этом случае сводится к задаче нелинейного программирования. Это означает, что ее нельзя свести к системе линейных уравнений, что усложняет задачу. Во втором подходе для каждого робота сначала производился поиск аттракторов — специальных точек на плоскости движения робота, задача которых «подсказывать» роботу как обойти препятствия на пути. Далее полученные результаты использовались для решения всей исходной задачи. Расчеты по двум подходам реализовали с помощью эволюционных алгоритмов и метода случайного поиска. Ученые провели 10 тестов для каждого из четырех эволюционных алгоритмов и метода случайного поиска и сравнили их работу.
Эффективность двух подходов и 5 алгоритмов (метод случайного поиска и 4 эволюционных алгоритма: генетический алгоритм, метод роя частиц, пчелиный алгоритм, и алгоритм серого волка) оценивалась на основе значения целевой функции — функции, которую нужно минимизировать в задаче оптимального управления. Чем оно меньше, тем лучше справился алгоритм. Для первого подхода все эволюционные алгоритмы оказались эффективнее метода случайного поиска. Лучше всех справился «метод роя частиц», значение целевой функции составило в среднем 5,5. Для метода случайного поиска это значение оказалось почти в три раза больше — 15,83. Для второго подхода метод случайного поиска также оказался наименее эффективным. Эволюционные алгоритмы сработали примерно одинаково эффективно. В одном из испытаний алгоритм серого волка дал минимальное значение целевой функции — 2,49.
«Не существует универсальных численных методов решения задач оптимального управления. Мы планируем подробнее изучить применение эволюционных алгоритмов и рассмотреть другие новые эволюционные алгоритмы, в том числе — гибридные», — Сергей Константинов, старший преподаватель департамента механики и процессов управления РУДН.
Результаты опубликованы в журнале Applied Sciences.
matematika_konstantinov_upravlenie_illyustr_2021-10-14.png
Представьте себе мир, где у каждого есть достаточно еды, чистая вода, доступ к образованию и достойная работа. Мир, где берегут природу и заботятся о будущем нашей планеты. Это и есть цели устойчивого развития — построить устойчивое будущее для всех! Для этого Организация Объединенных Наций (ООН) в 2015 году определила 17 Целей устойчивого развития (ЦУР). ЦУР — это глобальный план, который помогает странам и людям вместе двигаться к лучшему будущему. К нему присоединились 193 государства-члена ООН.
Исследователи факультета искусственного интеллекта РУДН провели масштабное исследование, которое раскрыло системные ошибки больших языковых моделей (LLM) при диагностике депрессии по тексту. Эта работа, выполненная совместно с коллегами из AIRI, ФИЦ ИУ РАН, ИСП РАН, МФТИ и MBZUAI, не только выявляет проблему, но и закладывает основу для создания более надёжных и безопасных инструментов для детектирования депрессии и тревожности.
В РУДН состоялась первая научно-практическая конференция «Функциональная морфология тканевого микроокружения: от теории к практике», посвящённая памяти академика РАН Михаила Пальцева. Она объединила ведущих исследователей из России, Китая и других стран, став важной площадкой для обсуждения трансляции фундаментальных открытий в персонализированную медицину.