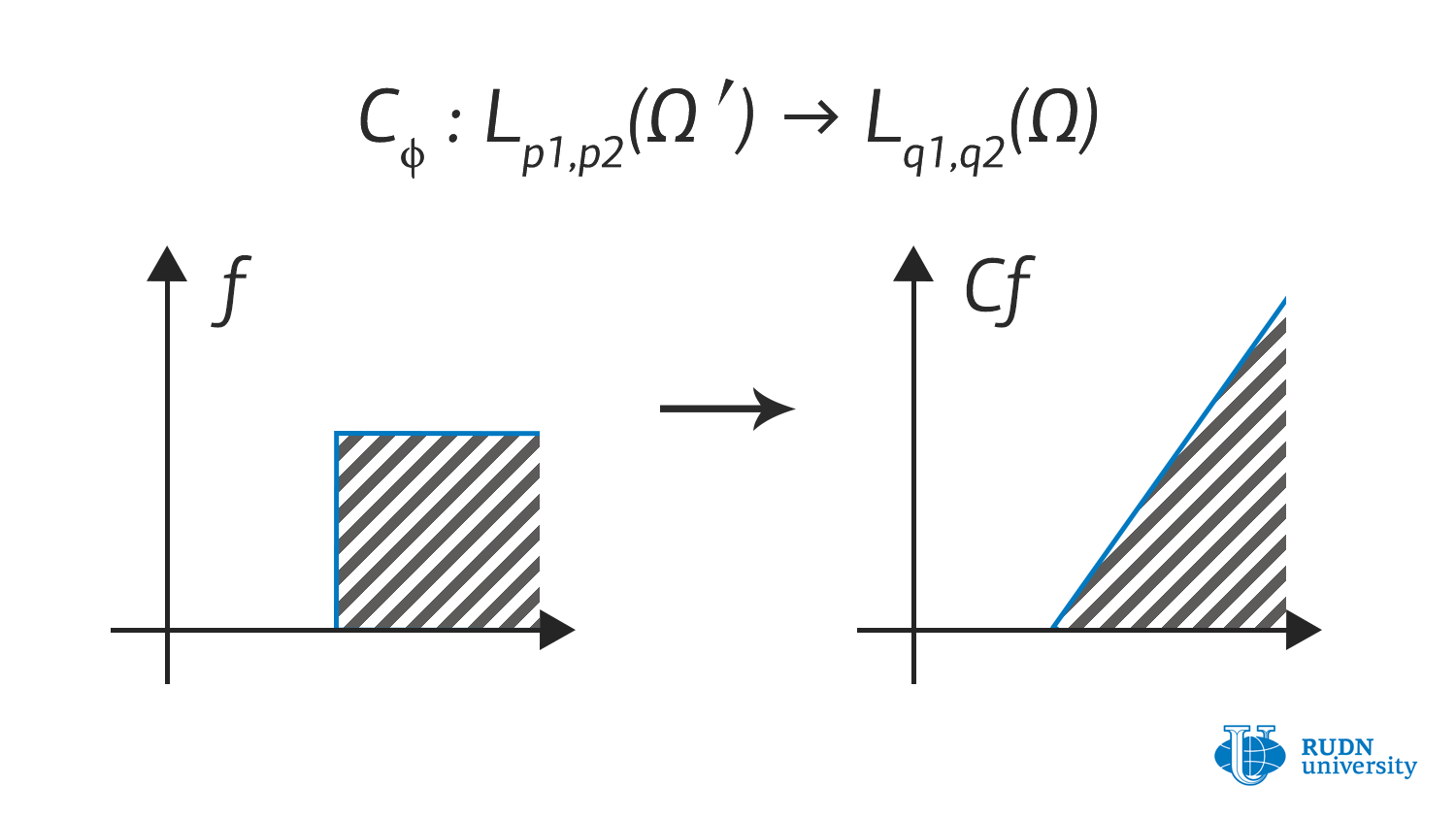Математики РУДН создали метод, который можно применять для изучения свойств пористых материалов
Так же как любая научно-инженерная область не может существовать без теории, современная наука о уравнениях
в частных производных имеет свою “теорию” - язык функционального анализа. Исследования функциональных пространств, в которых ищут решения уравнений, продолжаются с XIX века по наше время. Сначала люди научились применять теорию Фурье к решениям простейших линейных уравнений в частных производных, потом исследовали Банаховы и Гильбертовы пространства, а также пространства обобщенных функций - то, что по сути является языком квантовой механики.
Ближе к середине XX века были открыты пространства Соболева, которые занимают одно из центральных положений
в теории дифференциальных уравнений в частных производных. В течение последующих 50 лет с их помощью было найдено множество решений прикладных задач, которые невозможно обнаружить в обычных функциональных пространствах.
Ближе к началу XXI века возникла острая необходимость в новых методах исследования нелинейных уравнений
в частных производных - развились вычислительная математика и теория интегрируемых систем. Однако методы
из этих областей оказались слишком узконаправленными, и необходимость в развитии языка до сих пор никуда
не пропала.
Пространства Лебега со смешанными нормами оказываются более универсальным и гибким объектом в некоторых ситуациях. Эти пространства определяются так: берем пространство функций от нескольких переменных и определяем норму как повторное взятие норм Лебега с двумя разными параметрами. Они изначально возникли как одно
из обобщений пространств Лебега, и уже привлекли немало интереса со стороны теоретиков из нескольких стран Европы, а также Китая, Канады и России.
Ученые из Математического института РУДН Никита Евсеев и Александр Меновщиков развивают теорию операторов
для таких пространств, позволяющую применить их для прикладных задач, сформулированных на языке уравнений
в частных производных. Они получили массу новых результатов, описывающих свойства операторов на таких пространствах: критерии ограниченности операторов, свойства интегральных операторов, операторов умножения, операторов композиции и некоторых других. Также они получили некоторое количество вспомогательных результатов, полезных для дальнейшего развития этой области.
«Мы полагаем, что наши методы и результаты могут быть применены для в эволюционных задачах и дифференциальных задачах на не цилиндрических областях. Например, в (математической) биологии, где исследуется исследуемая поверхность или область меняется со временем, или в гидродинамике
для задач с переменной границей», — говорит Евсеев.
Разработки в этой области полезны для исследований уравнений Навье-Стокса - системы уравнений, описывающих
аэро- и гидродинамику. Пространства Лебега со смешанными нормами позволяют оценивать решения, что дает возможность, например, предсказать отсутствие турбулентности.
Полученные результаты также помогают исследовать прикладные задачи математической физики, возникающие
при исследовании пористых материалов и материалов с трещинами. К примеру, можно будет теоретически предсказать картину диффузии и теплопередачи в силикагелях, пористых стеклах, различных губках и пенах, а также в некоторых строительных материалах.
Статья в журнале Mathematical Notes.
Продолжаем делиться историями фронтовиков, которые после войны участвовали в создании Университета дружбы народов и воспитывали новое поколение студентов.
Игорь Васильевич Черемискин
В преддверии
В Москве прошёл XXXIII Российский национальный конгресс «Человек и лекарство» — главное ежегодное междисциплинарное событие в мире медицины, объединяющее науку, образование и клиническую практику. В этом году в числе лауреатов престижного конкурса молодых учёных — представитель медицинского института РУДН, ассистент кафедры общей врачебной практики Захар Иванов.